Question

Rod AB is made of a mild steel that is assumed to be elastoplastic with E = 200 GPa and σY = 345 MPa. After the rod has been attached to the rigid lever CD, it is found that end C is 6 mm too high. A vertical force Q is then applied at C until this point has moved to position C0 . Determine the required magnitude of Q and the deflection δ1 if the lever is to snap back to a horizontal position after Q is removed. HINT: "elastoplastic" means that rod AB is permanently deformed, and will not spring back to totally undeformed.

Answer 1

Q_max = 13.97 kN; δ1 = 3.39 mm

Step-by-step explanation:

(a) To calculated the required magnitude of Q, we have:

The area of the rod AB (
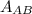`A_(AB)`)= (3.142*d^2)/4 = (3.142*0.009^2)/4 = 6.36*10^-5 m^2

Since the rod AB will be stretched permanently (i.e. elastoplastic).

The maximum force at rod AB is,
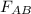`F_(AB)` = area of the rod AB * σY = (6.36*10^-5)*(345*10^6) = 21950.8 N

Summation (
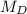`M_(D)`) = 0, Thus:

1.1*Q_max - 0.7*
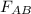`F_(AB)` = 0: 1.1*Q_max = 0.7*21950.8 = 15365.56

Therefore, Q_max = 15365.56/1.1 = 13968.69 N = 13.97 kN

(b) To estimate the deflection δ1 if the lever is to snap back to a horizontal position after Q is removed, we have:

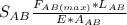`S_(AB) (F_(AB(max))*L_(AB))/(E*A_(AB) )` = (21950.8*1.25)/(200*10^9 * 6.36*10^-5) = 0.00216 m

Ф
`^(')` =
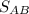`S_(AB)`/0.7 = 0.00216/0.7 = 0.0031 m

Thus, δ1 = 1.1*0.0031 = 0.00339 m = 3.39 mm