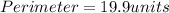
Why?
We can find the perimeter of any triangle adding the length of its sides. Since we are given 3 points, we need to calculate the length of the three sides of the triangle, and then add them to know the perimeter of the triangle.
Let be the points:
A(-3,-1)
B(-1,2)
C(6,1)
- Distances
From A to B:
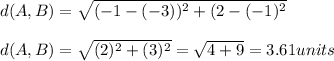
From A to C:
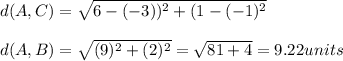
From B to C:
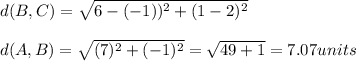
Now, calculating the perimeter, we have:
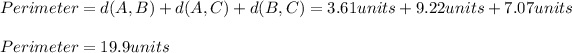
Have a nice day!