Question

Three tenths more than the product of -4 and a number less than 11.98. what could the number be?

Answer 1

Any number greater than -2.92 will satisfy the above condition.

One possible number could be -2 as -2 > -2.92.

Explanation:

Let the number be 'x'.

Given:

Three-tenths more than the product of -4 and the unknown number is less than 11.98.

Therefore, framing the above in equation form we get

Producto -4 and 'x' is
`-4x`

Three-tenths more than
`-4x` is
`-4x+(3)/(10)`

Now, the above expression is less than 11.98. So,

`-4x+(3)/(10)<11.98`

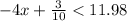
Solving for 'x', we add -
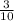`(3)/(10)` both sides,

`-4x<11.98-(3)/(10)\\-4x<11.98-0.3\\-4x<11.68`

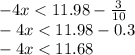
Now, dividing both sides by -4 will reverse the inequality sign. Therefore,

`x>(11.68)/(-4)\\x>-2.92`

Therefore, any number greater than -2.92 will satisfy the above condition.

So, one possible number could be -2 as -2 > -2.92.