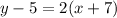Answer:
Therefore the equation of the line through ( -7 , 5 ) and ( -5 , 9) is
Linear Relationship i.e
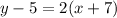
Explanation:
Given:
Let,
point A( x₁ , y₁) ≡ ( -7, 5 )
point B( x₂ , y₂) ≡ (-5, 9)
To Find:
Equation of Line AB =?
Solution:
Equation of a line passing through Two points A( x₁ , y₁) and B( x₂ , y₂)is given by the formula
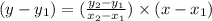
Substituting the given values in a above equation we get

Therefore the equation of the line through ( -7 , 5 ) and ( -5 , 9 ) is
Linear Relationship i.e