Answer:
The two numbers are 10 and 7.
Explanation:
Given:
The two numbers whose difference is three, when the larger number is decreased by three times the smaller number the result is -11.
Now, find the two numbers.
Let the larger number be
 .
.
Let the smaller number be
 .
.
As given, the two numbers whose difference is three:

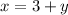
So, the value of
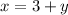 .
.
According to question:
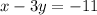
Putting the value of
 we get:
we get:
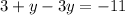
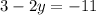
Moving variables on one side and the number on the other we get:
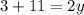

Dividing both sides by 2 we get:
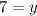
The smaller number = 7.
Now, putting the value of
 in the equation
in the equation
 :
:

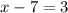
Adding both sides by 7 we get:
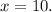
The larger number = 10.
Therefore, the two numbers are 10 and 7.