Question

A total of $11,000 is invested in two accounts. Part was invested at 4% and the rest was invested at 7%. If the investments earn $680 peer year, how much was invested at each rate? I=prt

Answer 1

The amount invested at 4% was $3,000 and the amount invested at 7% was $8,000

Explanation:

we know that

The simple interest formula is equal to

`I=P(rt)`

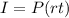
where

I is the Final Interest Value

P is the Principal amount of money to be invested

r is the rate of interest

t is Number of Time Periods

in this problem we have

`t=1\ year\\ P_1=x\\P_2=11,000-x\\I=\$680\\r_1=4\%=4/100=0.04\\r_2=7\%=7/100=0.07`

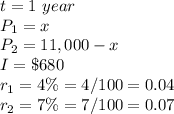
substitute in the formula above

`I=P_1(r_1t)+P_2(r_2t)`

`680=0.04x+(11,000-x)0.07`

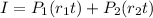
solve for x

`680=0.04x+770-0.07x`

`0.07x-0.04x=770-680`

`0.03x=90`

`x=\$3,000`

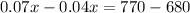
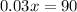
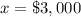
so

`\$11,000-x=\$11,000-\$3,000=\$8,000`

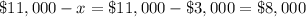
therefore

The amount invested at 4% was $3,000 and the amount invested at 7% was $8,000