Answer:
Δ PQT ~ Δ QRS .....{S-S-S test for similarity}...Proof is below.
Explanation:
Given:
In Δ PQT
PQ = 30 ft
QT = 28 ft
TP = 20 ft
In Δ QRS
QR = 15 ft
RS = 14 ft
SQ = 10 ft
To Prove:
Δ PQT ~ Δ QRS
Proof:
First we consider the ratio of the sides
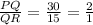 ..............( 1 )
..............( 1 )
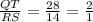 ..............( 2 )
..............( 2 )
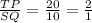 ..............( 3 )
..............( 3 )
So By equation ( 1 ), ( 2 ) and ( 3 ) we get
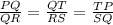
Now in Δ PQT and Δ QRS we have
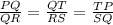
Which are corresponding sides of a similar triangle in proportion.
∴ Δ PQT ~ Δ QRS .....{S-S-S test for similarity}...Proved