Answer:
The standard deviation of the distribution is 492.847
Explanation:
Consider the provided information.
A city has 1,091,953 residents. A recent census showed that 364,656 of these residents regularly use the city's public transportation system.
Therefore the value of n is 1,091,953
The probability of success is:
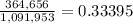
Calculate the standard deviation using the formula:
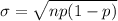
Substitute the respective values.
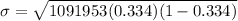
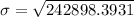

Hence, the standard deviation of the distribution is 492.847