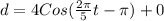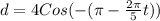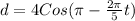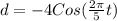Question

A buoy floating in the ocean is bobbing in simple harmonic motion with period 5 seconds and amplitude 4ft. Its displacement d from sea level at time =t0 seconds is −4ft, and initially it moves upward. (Note that upward is the positive direction.) Give the equation modeling the displacement d as a function of time t.

Answer 1

`d=-4Cos((2\pi)/(5)t)`

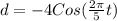
Explanation:

We are given that

Period =5 s

Amplitude=4 ft

Displacement d from sea level at time
`t=0s=-4 ft`

We have to find the modelling equation displacement d as a function of time.

We know that

The general equation of sinusoidal function is given by

`y(t)=Acos(Bt-C)+D`

B=
`(2\pi)/(period)=(2\pi)/(5)`

When t=0, y=d=-4 ft, D=0

Substitute the values then we get

`-4=4Cos((2\pi)/(5)(0)-C)+0`

`-4=4Cos(-C)`

`Cos(-C)=-1`

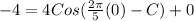
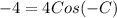
We know that Cos(-x)=Cos x

`Cos C=-1`

`Cos C=Cos \pi` (
`cos(\pi)=-1`)

`C=\pi`

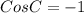
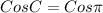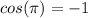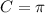
Substitute the values then, we get

`d=4Cos((2\pi)/(5)t-\pi)+0`

`d=4Cos(-(\pi-(2\pi)/(5)t))`

`d=4Cos(\pi-(2\pi)/(5)t)`

`Cos(\pi-x)=-Cosx`

`d=-4Cos((2\pi)/(5)t)`