Answer:
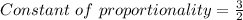
Explanation:
By definition, Direct proportion equations have the following form:

Where "k" is the Constant of proportionality.
The graph of a Direct proportional relationship is a straight line that passes through the origin.
In this case you need to pick any point on the line given in the picture. You can choose the following point:
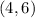
So, you can identify that:

Knowing that, you must substitute these values into the equation
 :
:
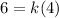
And finally, you need to solve for "k" in order to find its value. You get that this is:
