Question

You want to determine whether the amount of coffee that "coffee drinkers" consume on a weekly basis differs depending on whether the coffee drinker also smokes cigarettes. You seek 20 volunteers from your college campus to participate. Ten college students reported that they consume coffee but do not smoke cigarettes; these comprise the Coffee-Only group, or Group 1. Another ten college students reported that they consumed coffee and also smoked cigarettes; these comprise the Coffee + Cigarettes group, or Group 2. Then you ask them to monitor the frequency of 8 ounce cups of coffee they consumed over a seven day period. Which of the following are the correct statements of the null and alternate hypotheses, H0 and HA?

H0: µ1 > µ2 and HA: µ1 ≤ µ2
H0: µ1 ≤ µ2 and HA: µ1 > µ2
H0: µ1 < µ2 and HA: µ1 ≥ µ2
H0: µ1 ≥ µ2 and HA: µ1 < µ2
H0: µ1 = µ2 and HA: µ1 ≠ µ2
H0: µ1 ≠ µ2 and HA: µ1 = µ2

Answer 1

The correct option is e)
`H_0: \mu_1=\mu_2\ and\ H_a:\mu_1\\eq \mu_2`

Explanation:

Consider the provided information.

Ten college students reported that they consume coffee but do not smoke cigarettes; these comprise the Coffee-Only group, or Group 1. Another ten college students reported that they consumed coffee and also smoked cigarettes; these comprise the Coffee + Cigarettes group, or Group 2.

The null hypothesis tells the population parameter is equal to the claimed value.

If there is no statistical significance in the test then it is know as the null which is denoted by
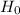`H_0`, otherwise it is known as alternative hypothesis which denoted by
`H_a`.

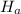The amount of coffee that "coffee drinkers" consume on a weekly basis differs depending on whether the coffee drinker also smokes cigarettes.

Thus, the required hypothesis are:
`H_0: \mu_1=\mu_2\ and\ H_a:\mu_1\\eq \mu_2`

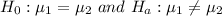
Therefore, the correct option is e)
`H_0: \mu_1=\mu_2\ and\ H_a:\mu_1\\eq \mu_2`