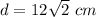Answer:
Explanation:
step 1
Find the length side of the square
we know that
The area of a square is equal to
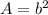
where
b is the length side
we have
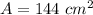
substitute in the formula of area
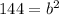
solve for b
square root both sides
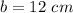
step 2
Find the length of the diagonal
Applying the Pythagorean Theorem
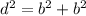
see the attached figure to better understand the problem
substitute the given values
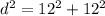
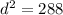
square root both sides
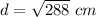
simplify