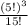Question

The Bernsteins, Hendersons, and Smiths each have five children. If the 15 children of these three families camp out in five different tents, where each tent holds three children, and the 15 children are randomly assigned to the five tents, what is the probability that every family has at least two of its children in the same tent?

Answer 1

Probability=1-
`((5!)^(3) )/(15!)`

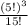
Explanation:

We have to solve this question with the help of complementary method. Observe the statement "Probability that every family has at least two of its children in the same tent". The complementary of this statement will be every family does not have atleast two of its children in the same tent ie. Each child of a family is not in the same tent as one from the same family.

P(A)=1-
`P(A)^(c)`

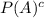
Therefore, we can get P(A) if we just take out the value of
`P(A)^(c)`

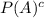
Probability=
`(TotalNo.OfFavourableOutcomes)/(TotalNo.ofOutcomes)`

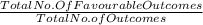
Imagine that we have 15 locations to fill and 15 people for it, so the total no. of cases= 15!

Bernstein's children can be arranged in 5 different tents in 5! ways.

Similarly Henderson's and Smith's children can be arranged in 5 different tents in 5! ways only.

Therefore,
`P(A)^(c)`=
`((5!)^(3) )/(15!)`

P(A)=1-
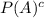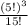
`((5!)^(3) )/(15!)`