Answer:
99% Confidence interval: (17.9064,19.8136)
Explanation:
We are given the following data set:
22,18,19,21,18,19,18,17,20,20,18,17,20,19,20,18,17,18,16,21,18,21
Formula:

where
 are data points,
are data points,
 is the mean and n is the number of observations.
is the mean and n is the number of observations.
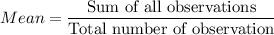
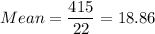
Sum of squares of differences = 52.59
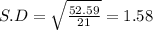
99% Confidence interval:
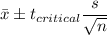
Putting the values, we get,
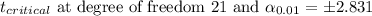
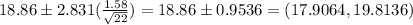
Option A) With 99% confidence, the mean miles per gallon in the population of 2008 SUVs is somewhere in the interval.