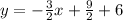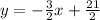Question

Consider the line y=-3/2x - 3

Find the equation of the line that is perpendicular to this line and passes through the point (3, 6).
Find the equation of the line that is parallel to this line and passes through the point (3, 6).

Answer 1

Part 1) Equation of a perpendicular line is
`y=(2)/(3)x+4`

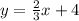
Part 2) Equation of a parallel line is
`y=-(3)/(2)x+(21)/(2)`

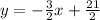
Explanation:

Part 1) Find the equation of the line that is perpendicular to the given line and passes through the point (3, 6).

we have

`y=-(3)/(2)x-3`

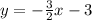
The slope of the given line is
`m=-(3)/(2)`

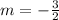
Remember that

If two lines are perpendicular, then their slopes are opposite reciprocal (the product of the slopes is equal to -1)

so

The slope of the perpendicular line to the given line is equal to

`m=(2)/(3)`

Find the equation of the line in point slope form

`y-y1=m(x-x1)`

we have

`m=(2)/(3)`

`point\ (3,6)`

substitute

`y-6=(2)/(3)(x-3)`

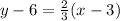
Convert to slope intercept form

`y=mx+b`

Isolate the variable y

`y-6=(2)/(3)x-2`

`y=(2)/(3)x-2+6`

`y=(2)/(3)x+4`

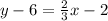
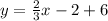
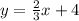
Part 2) Find the equation of the line that is parallel to the given line and passes through the point (3, 6).

we have

`y=-(3)/(2)x-3`

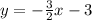
The slope of the given line is
`m=-(3)/(2)`

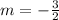
Remember that

If two lines are parallel, then their slopes are the same

so

The slope of the parallel line to the given line is equal to

`m=-(3)/(2)`

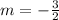
Find the equation of the line in point slope form

`y-y1=m(x-x1)`

we have

`m=-(3)/(2)`

`point\ (3,6)`

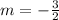
substitute

`y-6=-(3)/(2)(x-3)`

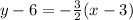
Convert to slope intercept form

`y=mx+b`

Isolate the variable y

`y-6=-(3)/(2)x+(9)/(2)`

`y=-(3)/(2)x+(9)/(2)+6`

`y=-(3)/(2)x+(21)/(2)`