Question

Two straight roads intersect at right angles. A car is traveling south toward the intersection while a radar-monitored-speed sign is positioned mile east of the intersection. The speed sign provides both the distance from the sign to an approaching car and the rate at which the distance between the sign and the car is changing. At a certain time, the speed sign shows that the approaching car is exactly mile away from the sign and that the rate at which the car is traveling toward the intersection is 60 miles per hour. Which of the following is true about the distance between the car and the intersection at this instant? A ) The distance is increasing at a rate of miles per hour. B) The distance is decreasing at a rate of miles per hour. The distance is increasing at a rate of miles per hour. D The distance is decreasing at a rate of miles per hour.

Answer 1

So, first of all, there is some information missing to the posted problem, since there no data about some distances and velocities. The actual problem should look something like this:

"Two straight roads intersect at right angles. A car is traveling south toward the intersection while a radar-monitored-speed sign is positioned 1/4 mile east of the intersection. The speed sign provides both the distance from the sign to an approaching car and the rate at which the distance between the sign and the car is changing. At a certain time, the speed sign shows that the approaching car is exactly 1/2 mile away from the sign and that the rate at which the car is traveling toward the intersection is 60 miles per hour. Which of the following is true about the distance between the car and the intersection at this instant?

A ) The distance is increasing at a rate of
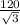`(120)/(√(3))` miles per hour.

B) The distance is decreasing at a rate of
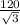`(120)/(√(3))` miles per hour.

C) The distance is increasing at a rate of
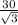`(30)/(√(3))` miles per hour.

D) The distance is decreasing at a rate of
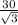`(30)/(√(3))`miles per hour."

Of course, the values might be different but the procedure is exactly the same.

Answer:

B) The distance is decreasing at a rate of
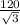`(120)/(√(3))` miles per hour.

Explanation:

In order to solve this problem, we must first do a drawing of the situation, which should help us visualize the situation better so we can do an analysis of it. (See attached picture).

So, as you may see, the problem can be simplified to a right triangle. A right triangle can be modeled by using Pythagore, so we get that:

`d^(2)=x^(2)+y^(2)`

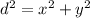
From what the problem tells us, the distance beween the radar and the car will change over time, just like the distance between the car and the intersection. The x-value (the distance between the radar and the intersection) will remain constant, so we can directly substitute that value into our equation:

`d^(2)=((1)/(4))^(2)+y^(2)`

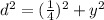
Which yields:

`d^(2)=(1)/(16)+y^(2)`

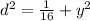
Now, we can use this equation to figure out the distance between the car and the intersection when d=1/2 mi, so we get:

`((1)/(2))^(2)=(1)/(16)+y^(2)`

when solving for y we get:

`y=\sqrt{(1)/(4)-(1)/(16)}`

which yields:

`y=(√(3))/(4)`

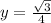
We are not going to use this value yet, but we will need it to find the final answer.

Now, we had the pythagorean equation to be:

`d^(2)=(1)/(16)+y^(2)`

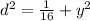
now we can take the implicit derivative of this equation, so we get:

`2d (dd)/(dt)=2y (dy)/(dt)`

which will describe the velocity of the car with respect to the radar and with respect to the intersection. We can simplify it by dividing both sides of the equation into two, so we get:

`d (dd)/(dt)=y (dy)/(dt)`

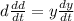
and now we can solve for
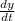`(dy)/(dt)` which represents the velocity of the car with respect to the intersection:

`(dy)/(dt)=(d)/(y) (dd)/(dt)`

in this case:

d=1/2 mi

`y=(√(3))/(4)`

`(dd)/(dt)=-60mph`

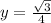
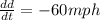
dd/dt is negative because the car is approaching the radar. In other words, the distance between the car and the radar is decreasing.

so we proceed and do the substitutions:

`(dy)/(dt)=(1/2)/(√(3)/4) (-60)`

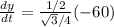
which simplifies to:

`(dy)/(dt)=(2)/(√(3)) (-60)`

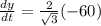
which yields:

`(dy)/(dt)=-(120)/(√(3))`

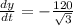
the negative sign means that the distance between the car and the intersection is decreasing, so the answer is:

B) The distance is decreasing at a rate of
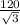`(120)/(√(3))` miles per hour.