Question

A report states that the mean yearly salary offer for students graduating with a degree in accounting is $48,743. Suppose that a random sample of 50 accounting graduates at a large university who received job offers resulted in a mean offer of $49,870 and a standard deviation of $3300. Do the sample data provide strong support for the claim that the mean salary offer for accounting graduates of this university is higher than the national average of $48,743? Test the relevant hypotheses using α = 0.05. (Use a statistical computer package to calculate the P-value. Round your test statistic to two decimal places and your P-value to three decimal places.) t = P-value = State your conclusion. Do not reject H0. We have convincing evidence that the mean salary offer for accounting graduates of this university is higher than the national average of $48,743. Reject H0. We do not have convincing evidence that the mean salary offer for accounting graduates of this university is higher than the national average of $48,743. Do not reject H0. We do not have convincing evidence that the mean salary offer for accounting graduates of this university is higher than the national average of $48,743. Reject H0. We have convincing evidence that the mean salary offer for accounting graduates of this university is higher than the national average of $48,743.

Answer 1

Answer: Reject H0. We do not have convincing evidence that the mean salary offer for accounting graduates of this university is higher than the national average of $48,743

Explanation:

The relevant t-test for this situation would be:

`(49870-48743)/((3300)/(√(50) ) )`

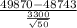
Which is (49870-48743) ÷ standard error

standard error = standard deviation ÷√sample size

From the t-test, we obtain the value = 2.41...

Using α = 0.05, our critical value is 1.96. As 2.41 is larger than 1.96, we reject our null hypothesis that the mean salary offer is higher than $48,743