Answer:

Explanation:
Given inequality:
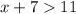
We need to solve the given inequality for solutions of
 .
.
In order to solve for the inequality, we will isolate
 in one side of the in-equation.
in one side of the in-equation.
We have,
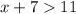
Subtracting both sides by 7.
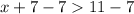

Thus, the solution of the given inequality is all real numbers greater than 4.
The solution in interval form can be written as (4,∞).
The graph for the inequality is shown below.