Question

A ball is rolled at an initial speed of 5 m/s and finishes a certain distance at a speed of 7 m/s. if the ball rolled for 9 seconds then how long was this distance that the ball rolled?

Answer 1

The ball rolled a distance of 54 m.

Step-by-step explanation:

Given:

Initial velocity of the ball is,
`u=5\ m/s`

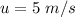
Final velocity of the ball is,
`v=7\ m/s`

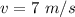
Time for rolling is,
`t=9\ s`

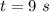
The distance of rolling is,
`S=?`

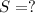
First, let us find the acceleration of the ball using Newton's equation of motion as:

`v=u+at\\a=(v-u)/(t)\\a=(7-5)/(9)=(2)/(9)\ m/s^2`

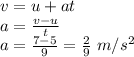
Now, displacement of the ball can be determined using the following equation of motion:

`v^2=u^2+2aS`

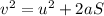
Rewriting the above in terms of 'S', we get

`S=(v^2-u^2)/(2a)`

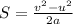
Plug in the known values and solve for 'S'. This gives,

`S=(7^2-5^2)/(2* (2)/(9))\\\\S=(49-25)/((4)/(9))\\\\S=(9* 24)/(4)\\\\S=9* 6=54\ m`

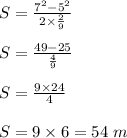
Therefore, the ball rolled a distance of 54 m.