Question

A)A certain medical machine emits x-rays with a minimum wavelength of 0.024 nm. One day, the machine has an electrical problem and the voltage applied to the x-ray tube decreases to 76% of its normal value. Now what is the minimum x-ray wavelength produced by the machine?

lmin = ___________nm

(b) What is the maximum x-ray energy this machine (with electrical problems) can produce?

Emax =___________ eV

(c) The atomic number of an element is 82. According to the Bohr model, what is the energy of a Ka x-ray photon?

E =_______________ eV

Answer 1

(a) 0.032 nm

(b) 39,235 eV

(c) 70,267.8 eV

Step-by-step explanation:

(a) The energy of a photon can be calculated using:

E = hc/λ equation (1)

where:

h = 4.13*10^-15 eV.s

c = 3*10^8 m/s

λ = 0.024*10^-9 m

Thus:

E = (4.13*10^-15)*(3*10^8)/0.024*10^-9 = 51,625 eV

Then we calculate 76% of this estimated energy and determine the new wavelength:

`E_(new) = 0.76*51625 = 39,235 eV`

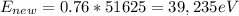
Using equation (1) to determine the new wavelength:

λ
`_(new) = (h*c)/(E_(new) )`

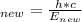
λ
`_(new)` = (4.13*10^-15)*(3*10^8)/39235 = 3.15*10^-11 m = 0.032 nm

(b) As calculated in part (a), the maximum x-ray energy this machine can produce is
`E_(new) = 0.76*51625 = 39,235 eV`

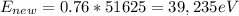
(c) The energy of a Ka x-ray photon can be estimated using:

`E_(ka) = (10.2 eV)*(Z-1)^(2)`

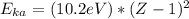
where Z is the atomic number = 84.

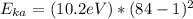`E_(ka) = (10.2 eV)*(84-1)^(2)` = 70,267.8 eV