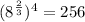Answer:
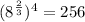
Explanation:
Given
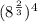
Required
Simplify
To simplify this, we apply law of indices but first we start by solving the expression in bracket.
8 =2 * 2 * 2
8 = 2³
So, we substitute 2³ for 8
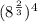 becomes
becomes

From law of indices
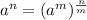 ==>
==>
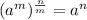
So,
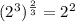
At this point we have
 =
=
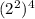
Also, from law of indices

So,
 =
=
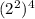
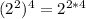

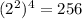
Hence,