Question

An asteroid is in an elliptical orbit around a distant star. At its closest approach, the asteroid is 0.540 AU from the star and has a speed of 54.0 km/s. When the asteroid is at its farthest distance from the star of 32.0 AU, what is its speed (in km/s)? (1 AU is the average distance from the Earth to the Sun and is equal to 1.496 ✕ 1011 m. You may assume that other planets an

Answer 1

0.91125 km/s

Step-by-step explanation:

`v_1` = Velocity of planet initially = 54 km/s

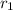`r_1` = Distance from star = 0.54 AU

`v_2` = Final velocity of planet

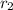`r_2` = Final distance from star = 32 AU

As the angular momentum of the system is conserved

`mv_1r_1=mv_2r_2\\\Rightarrow v_1r_1=v_2r_2\\\Rightarrow v_2=(v_1r_1)/(r_2)\\\Rightarrow v_2=(54* 0.54)/(32)\\\Rightarrow v_2=0.91125\ km/s`

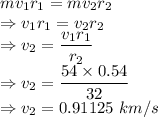
When the exoplanet is at its farthest distance from the star the speed is 0.91125 km/s