Question

Find the initial value aa, growth/decay factor bb, and growth/decay rate rr for the following exponential function: Q(t)=0.0019(2.22)−3t Q(t)=0.0019(2.22)−3t (a) The initial value is a=a= help (numbers) (b) The growth factor is b=b= help (numbers) (Retain at least four decimal places.) (c) The growth rate is r=r= % help (numbers) (Ensure your answer is accurate to at least the nearest 0.01%) (Note that if rr gives a decay rate you should have r<0r<0.)

Answer 1

a) 0.0019

b) 0.0913

c) 9.13%

Explanation:

We are given the following information in the question:

`Q(t)=0.0019(2.22)^(-3t)`

The standard form of exponential function is

`f(t) = ab^(t)`

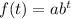
where a is the initial amount and b is the base.

Rewriting the the given function, we have:

`Q(t)=0.0019(2.22)^(-3t)\\Q(t)=0.0019((2.22)^(-3))^t\\Q(t)=0.0019(0.0913)^t`

a) Initial Value

Putting t = 0, we get,

`Q(0)=0.0019(0.0913)^0 = 0.0019`

a = 0.0019

b) Growth factor

Comparing, we get, b = 0.0913

c) Growth rate

`\text{Growth factor}* 100\% = 0.0913* 100\% = 9.13\%`