Question

Approximately 80,000 marriages took place in the state of New York last year. Estimate the probability that, for at least one of these couples, (a) both partners were born on April 30; (b) both partners celebrated their birthday on the same day of the year. State your assumptions.

Answer 1

a) There is a 45.12% probability that, for at least one of these couples, both partners were born on April 30.

b) There is a 100% probability that, for at least one of these couples, both partners were born on the same day.

Explanation:

For each couple, either they have the same birth date, or they do not. This means that we solve this problem using the binomial probability distribution.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

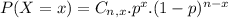
In which
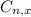`C_(n,x)` is the number of different combinatios of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

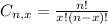
And p is the probability of X happening.

In this problem we have that:

There are 80000 couples, so
`n = 80000`.

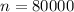The probability that a couple was born on April 30 is
`p = (1)/(365)*(1)/(365) = 0.0000075`

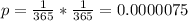
Estimate the probability that, for at least one of these couples, (a) both partners were born on April 30;

This is
`P(X > 0) = 1 - P(X = 0)`

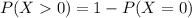
So

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(80000,0).(0.0000075)^(0).(1-0.0000075)^(80000) = 0.5488`

`P(X > 0) = 1 - P(X = 0) = 1 - 0.5488 = 0.4512`

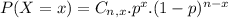
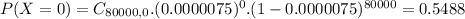
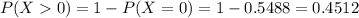
There is a 45.12% probability that, for at least one of these couples, both partners were born on April 30.

(b) both partners celebrated their birthday on the same day of the year.

There are 365 days on the year. So the probability that a couple was born on the same day is
`p = 365*(1)/(365)*(1)/(365) = 365*0.0000075 = 0.0027`

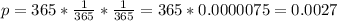
So:

`P(X > 0) = 1 - P(X = 0)`

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(80000,0).(0.0027)^(0).(1-0.0027)^(80000) = 1 * 10^(-94) = 0`

`P(X > 0) = 1 - P(X = 0) = 1 - 0 = 1`

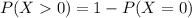
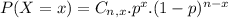
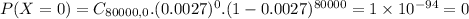
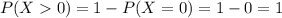
There is a 100% probability that, for at least one of these couples, both partners were born on the same day.