Question

Suppose that on a hot and sticky afternoon in the spring, a tornado passes over the high school. If the air pressure in the lab (volume of 180m3) was 1.1 atm before the storm and 0.85 atm during the storm, to what volume would the laboratory try to expand in order to make up for the large pressure difference outside?

a. 190m3
b. 230m3
c. 1,800m3
d. 7,100m3

Answer 1

232.9m³ (Option b. is the closest answer)

Step-by-step explanation:

Given:

Air pressure in the lab before the storm, P₁ = 1.1atm

Air volume in the lab before the storm, V₁ = 180m³

Air pressure in the lab during the storm P₂ = 0.85atm

Air volume in the lab before the storm, V₂ = ?

Applying Boyle's law: P₁V₁ = P₂V₂ (at constant temperature)

`V_(2) = (P_(1)V_(1))/(P_(2))`

`V_(2) = (1.1 * 180)/(0.85)`

`V_(2) = (198)/(0.85)`

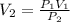
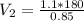
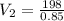
V₂ = 232.9m³

The air volume in the laboratory that would expand in order to make up for the large pressure difference outside is 232.9m³