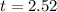Question

A biologist observed that a certain bacterial colony obeys the population growth law and that the colony triples every 4 hours.

If the colony occupied 2 square centimeters initially, find:

(a) An expression for the size P(t) of the colony at any time t.

(b) The area occupied by the colony after 12 hours.

(c) The doubling time for the colony?

Answer 1

a)
`P(t) = 2e^(0.275t)`

b) 54.225 square centimeters.

c) 2.52 hours

Explanation:

The population growth law is:

`P(t) = P_(0)e^(rt)`

In which P(t) is the population after t hours,
`P_(0)` is the initial population and r is the growth rate, as a decimal.

In this problem, we have that:

The colony occupied 2 square centimeters initially, so
`P_(0) = 2`

The colony triples every 4 hours. So

`P(4) = 3P_(0) = 6`

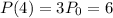
(a) An expression for the size P(t) of the colony at any time t.

We have to find the value of r. We can do this by using the P(4) equation.

`P(t) = P_(0)e^(rt)`

`6 = 2e^(4r)`

`e^(4r) = 3`

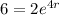
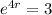
Applying ln to both sides, we get:

`4r = 1.1`

`r = 0.275`

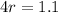
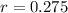
So

`P(t) = 2e^(0.275t)`

(b) The area occupied by the colony after 12 hours.

`P(t) = 2e^(0.275t)`

`P(12) = 2e^(0.275*12)`

`P(12) = 54.225`

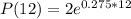
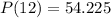
(c) The doubling time for the colony?

t when
`P(t) = 2P_(0) = 2*2 = 4`.

`P(t) = 2e^(0.275t)`

`4 = 2e^(0.275t)`

`e^(0.275t) = 2`

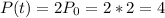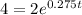
Applying ln to both sides

`0.275t = 0.6931`

`t = 2.52`