Question

Amy has $1,000 in a savings account at the beginning of the fall. She wants to have at least $500 in the account by the end of the fall. She withdraws $100 a week for living expenses. Write an inequality for the number of weeks Amy can withdraw money, and solve.

A) 1000 - 100w ≤ 500; w ≥ 6
B) 1000 + 100w ≤ 500; w ≤ 5
C) 1000 + 100w ≥ 500; w ≥ 6
D) 1000 - 100w ≥ 500; w ≤ 5

Answer 1

D.
`1000 - 100w \geq 500; w \leq 5`

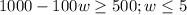
Explanation:

Given:

Initial amount in the bank = $1000

Money withdrawn each week = $100

Final amount should be at least $500.

Now, let the number of weeks the money is withdrawn be 'w'.

Therefore,

Money withdrawn in 'w' weeks =
`\textrm{Money withdrawn each week}* w`

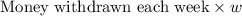
Total Money withdrawn in 'w' weeks =
`100w`

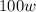
Now, final amount after 'w' weeks is equal to the difference between initial amount and total withdrawal amount. Therefore,

Final amount = Initial amount - Total withdrawal amount

Final amount =
`1000 - 100w`

Now, final amount must be greater than or equal to $500. So,

`\textrm{Final amount}\geq500\\\\1000-100w\geq500`

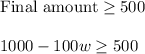
Therefore, the inequality that represents the inequality for the number of weeks Amy can withdraw money is:

`1000-100w\geq500`

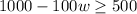
Now, let us solve for 'w'.

Adding -500 and 100w both sides, we get:

`1000-500-100w+100w\geq500-500+100w\\\\500\geq100w\\\\\textrm{The above inequality is reversed when taking 100w on the left side}\\\\100w\leq500\\\\w\leq(500)/(100)\\\\\therefore w\leq5`

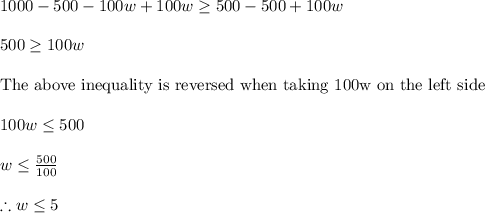
Therefore, the correct option is (D).