Answer:
Therefore,
Distance between XY is 878 ft and YB is 524 ft.
Explanation:
Given:
BW = 1612 ft
∠ Y = 72°
∠ X = 49°
To Find:
XY = ?
YB = ?
Solution:
In right angle Triangle Δ WBY Tangent identity,
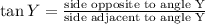
Substituting we get
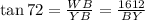
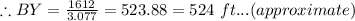
Similarly,
In right angle Triangle Δ WBX Tangent identity,
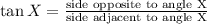
Substituting we get
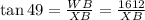
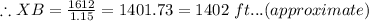
Now For
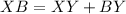 .............Addition Property
.............Addition Property
Substituting we get
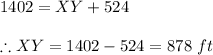
Therefore
Distance between XY is 878 ft and YB is 524 ft.