Question

a concert venue can hold 200 people. student tickets are 50% less than adult tickets. Adult tickets at $50.00. The venue was sold out and made a revenue of $9125 for one event. How many adults vs. student tickets were sold?

Answer 1

The number of adult tickets sold is 165 and number of students tickets sold were 35

Solution:

Let "a" be the number of adult tickets sold

Let "s" be the number of student tickets sold

Cost of 1 adult ticket = $ 50.00

Student tickets are 50% less than adult tickets

Cost of 1 student ticket = Cost of 1 adult ticket - 50 % of Cost of 1 adult ticket

`\rightarrow 50.00 - 50 \% \text{ of } 50.00\\\\\rightarrow 50 - (50)/(100) * 50\\\\\rightarrow 50 - 25 = 25`

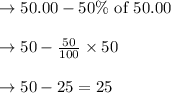
Thus Cost of 1 student ticket = $ 25

Given that a concert venue can hold 200 people

So we get,

number of adult tickets sold + number of student tickets sold = 200

a + s = 200 ----- eqn 1

The venue was sold out and made a revenue of $9125 for one event

So we can frame a equation as:

number of adult tickets sold x Cost of 1 adult ticket + number of student tickets sold x Cost of 1 student ticket = $ 9125

`a * 50.00 + s * 25 = 9125`

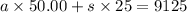
50a + 25s = 9125 ---- eqn 2

Let us solve eqn 1 and eqn 2 to find values of "a" and "s"

From eqn 1,

a = 200 - s --- eqn 3

Substitute eqn 3 in eqn 2

50(200 - s) + 25s = 9125

10000 - 50s + 25s = 9125

-25s = 9125 - 10000

-25s = -875

s = 35

Substitute s = 35 in eqn 3

a = 200 - 35

a = 165

Thus the number of adult tickets sold is 165 and number of students tickets sold were 35