Question

Given the perimeter of the given shape, find the length of each side of the object.

1) A triangle where the perimeter is 25 inches. The length of the sides are 2w+1, 3w and 3w.

Answer 1

The length of each side is 17 in, 24 in, 24 in.

Explanation:

Given,

Perimeter of the triangle =
`25\ in`

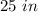
Length of 1st side =
`2w+1`

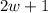
Length of 2nd side =
`3w`

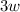
Length of 3rd side =
`3w`

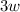
The perimeter of a triangle is equal to the sum of the length of all the three sides of the triangle.

Perimeter of the triangle = Length of 1st side + Length of 2nd side + Length of 3rd side

Now substituting the given values, we get;

`2w+1+3w+3w=25\\\\8w+1=25\\\\8w=25-1\\\\8w=24\\\\w=(24)/(8)=3`

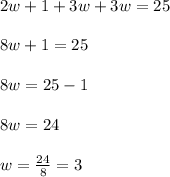
Now we have the value of w so we can calculate the length of each side.

Length of 1st side =
`2w+1=2*8+1=16+1=17\ in`

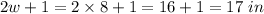
Length of 2nd side =
`3w=3*8=24\ in`

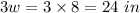
Length of 3rd side =
`3w=3*8=24\ in`

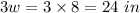
Thus the length of each side is 17 in, 24 in, 24 in.