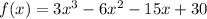Question

Which is the polynomial function of lowest degree with rational real coefficients, a leading coefficient of 3 and roots StartRoot 5 EndRoot and 2?

Answer 1

`f(x)=3x^3-6x^2-15x+30`

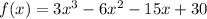
Or

`f(x)=3(x-2)(x+√(5))(x-√(5))`

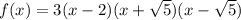
Explanation:

For a polynomial function of lowest degree with rational real coefficients, each root has multiplicity of 1.

The polynomial has roots
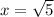`x=√(5)` and 2 with a leading coefficient of 3.

By the irrational root theorem of polynomials,
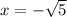`x=-√(5)` is also a root of the required polynomial.

By the factor theorem, we can write the polynomial in factored form as:

`f(x)=3(x-2)(x+√(5))(x-√(5))`

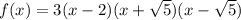
We expand, applying difference of two squares to obtain

`f(x)=3(x-2)(x^2-5)`

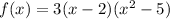
We expand further using the distributive property to get:

`f(x)=3x^3-6x^2-15x+30`

Answer 2

A on edgegentuyuyuyuy

Explanation: