Question

Point A is (3,4) Point B is (-1,-2). Find the coordinates of point Q along the directed line segment AB so that the ratio of AQ to QB is 4 to 2.

Answer 1

The Co ordinates of Point Q is (0.33,0).

Explanation:

Given,

Co ordinates of Point A = (3,4)

Co ordinates of Point B = (-1,-2)

We have to find out the co ordinates of point Q that divides the line segment in the ratio of 4:2.

Solution,

For finding the co ordinates of Q, we use the section formula.

`Q(x,y)=((mx_2+nx_1)/(m+n)) ((my_2+ny_1)/(m+n))`

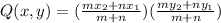
Here,

`x_1=3\ \ \ x_2=-1\\y_1=4\ \ \ y_2=-2\\m=4\ \ and\ \ n=2`

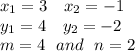
Now we substitute the given values and get;

`Q(x,y)=((4*-1+2*3)/(4+2)) ((4*-2+2*4)/(4+2))\\\\Q(x,y)=((-4+6)/(6))((-8+8)/(6))\\\\Q(x,y)=((2)/(6))((0)/(6))\\\\Q(x,y)=(0.33,0)`

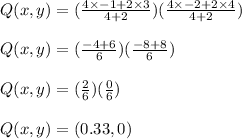
Hence The Co ordinates of Point Q is (0.33,0).