Question

Which table represents the same proportional relationship as the equation y=36x

Answer 1

The table in the attached figure

Explanation:

we know that

A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
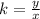`k=(y)/(x)` or
`y=kx`

we have

`y=36x`

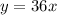
The constant of proportionality of the given equation is k=36

so

The table that represents the same proportional relationship as the given equation in the attached figure

because

Find the value of the constant of proportionality k

For x=0.5,y=18 --->
`k=(18)/(0.5)=36`

For x=2,y=72 --->
`k=(72)/(2)=36`

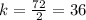
For x=3,y=108 --->
`k=(108)/(3)=36`

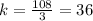
For x=6,y=216 --->
`k=(216)/(6)=36`

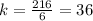
The constant of proportionality k is the same that the given equation