Answer: At-least 88.89%
Explanation:
As per given , we have
Population mean :
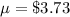
Standard deviation :
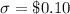
Now , $3.43= $3.73- 3(0.10) =
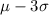
$4.03 = $3.73+3(0.10) =
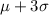
i.e. $3.43 is 3 standard deviations below mean and $4.03 is 3 standard deviations above mean .
To find : the minimum percentage of stores that sell a gallon of milk for between $3.43 and $4.03.
i.e. to find minimum percentage of stores that sell a gallon of milk lies within 3 standard deviations from mean.
According to Chebyshev, At-least
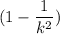 of the values lies with in
of the values lies with in
 from mean.
from mean.
For k= 3
At-least
 of the values lies within
of the values lies within
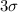 from mean.
from mean.
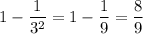
In percent =
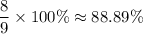
Hence, the minimum percentage of stores that sell a gallon of milk for between $3.43 and $4.03 = At-least 88.89%