Question

An automobile (and its occupants) of total mass M = 2000 kg, is moving through a

curved dip in the road of radius R = 20 m at a constant speed v = 20 m/s. For this analysis, you can
neglect air resistance. Consider the automobile (and its occupants) as the system of interest. Use g =
10 m/s2.


Calculate the normal force exerted by the road on the system (car and its occupants).
A) 60,000 N
B) 20,000 N
C) 40,000 N
D) 50,000 N
E) 30,000 N

Answer 1

Normal force, N = 60000 N

Step-by-step explanation:

It is given that,

Mass of the automobile, m = 2000 kg

Radius of the curved road, r = 20 m

Speed of the automobile, v = 20 m/s

Let N is the normal and F is the net force acting on the automobile or the centripetal force. It is given by :

`N-mg=(mv^2)/(r)`

`N=(mv^2)/(r)+mg`

`N=m((v^2)/(r)+g)`

`N=2000* (((20)^2)/(20)+10)`

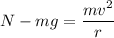
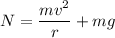
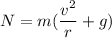
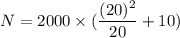
N = 60000 N

So, the normal force exerted by the road on the system is 60000 Newton. Hence, this is the required solution.