Question

Use the given data to find the minimum sample size required to estimate a population proportion or percentage. Margin of error: seven percentage points, confidence level 95%, from a prior study,^p is estimated by the decimal equivalent of 42%n=_____ (round to the nearest integer.)

Answer 1

Answer: 191

Explanation:

Formula to find the minimum sample size required to estimate a population proportion or percentage:

`n= \hat{p}(1-\hat{p})((z^*)/(E))^2`

, where
`\hat{p}` = proportion estimated by prior study.

E= Margin of error.

z* = Critical z-value.

Given : Confidence level = 95%

Critical value for 95% confidence = z*=1.96

`\hat{p}=\ 42\%=0.42`

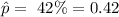
E= 7%= 0.07

Then,
`n= 0.42(1-0.42)((1.96)/(0.07))^2`

`n= 0.42(0.58)(28)^2`

`n= 0.2436(784)=190.9824approx191`

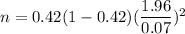
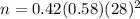
Hence, the minimum sample size required=191