Question

Find the parametric and symmetric equations for the line passing through the points P1=(2,2,3) and P2=(1,3,−1) . NOTE: this problem does not have a unique answer unless we specify how to choose the direction vector v (see pages 610 and 611). In order to obtain the required solution for this problem use the vector v=P1−P2 (see page 585). Further, you need to use the given point P1 in the formula. PARAMETRIC: x(t)= y(t)= z(t)= SYMMETRIC: (quotient involving x ) = (quotient involving y) = (quotient involving z ) =

Answer 1

parametric equation: q = (2-t)x + (2+t)y + (3-4t)z

symm equation:
`(x-2)/(-1) = (y-2)/(1) = (z-3)/(-4)`

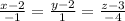
Explanation:

Parametric equation is just like the point slope equation:

y= b + mx

but in this case we have multiple variable so it'll be

q= p₀ + dt

p₀ will be any of your point. d will be the vector containing points shared by both your vector. It can be found by subtracting your two points together.

t is just an arbitrary variable.

Solve for d=p₂ - p₁ , you can also do d=p₁ - p₂

Now plug it into your q= p₀ + dt equation.

You can plug p₂ or p₁ in for p₀. I used p₁.

The result should give you the parametric equation.

Now solve for all of them in term of t. This step is just basic algebra.

since they're all t=..., then you can set them all equal to each other to get the symmetric equation.