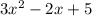Answer:
Answer:The correct option is A).
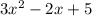
Given of x value and respective f(x) are
x f(x)
-1 10
0 5
2 13
To find f(x):
Given that f(x) is a parabola.
we know that parabola is polynomial of degree 2
The equation of parabola is ax^2+bx+c=0
For x=(-1) and f(x)=10
f(x)=
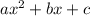
f(-1)=
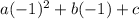
10=
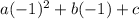
a-b+c=10 Equation 1
For x=0 and f(x)=5
f(x)=
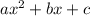
f(0)=
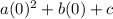
c=5 Equation 2
For x=2 and f(x)=13
f(x)=
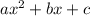
f(2)=
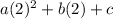
13=
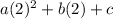
4a+2b+c=13 Equation 3
From equation 1 and equation 2,
a-b+c=10 and c=5
a-b+c=10
a-b+5=10
a-b=(5)
From equation 3 and equation 2,
4a+2b+c=13 and c=5
4a+2b+c=13
4a+2b+5=13
4a+2b=8
For value of a and b:
Equation 4: a-b=(5)
Equation 4: a-b=(5)Equation 5: 4a+2b=8
We write as,
4a+2b=8
4(5+b)+2b=8
(20+4b)+2b=8
20+6b=8
6b=-12
b=(-2)
hence,
a-b=(5)
a-(-2)=(5)
a=3
Therefore, the value of a =3, b=(-2) and c=5
Thus,
The equation of a f(x) is
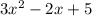
The correct option is A).