Question

A rectangular pen is made with 200m of fencing on three sides. The fourth side is a stone wall. Determine the greatest possible area of such an enclosure

Answer 1

5000 sq. meters.

Explanation:

Let the length of the rectangle is L m and width is W m.

Now, if the fourth side is a length of the rectangle, then by the condition given,

L + 2W = 200

⇒ L = 200 - 2W

Now, area of the rectangle is A = LW = (200 - 2W)W

For, area to be maximum the condition is

`(dA)/(dW) = 0 = 200 - 4W`

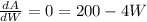
⇒ W = 50 m.

Then, L = 200 - 2W = 100 m.

Therefore, the maximum are is
`A_(max) = 50 * 100 = 5000` sq. meters. (Answer)