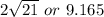Answer:
The diagonal of the given regular solid is
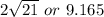
Explanation:
Given:
The given regular solid is a cuboid or a rectangular prism.
Length of the cuboid is,
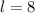
Width of the cuboid is,
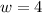
Height of the cuboid is,
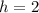
We know that, for a cuboid of length 'l', width 'w' and height 'h', the diagonal length 'd' is given as:

Plug in 8 for 'l', 4 for 'w', 2 for 'h' and solve for 'd'. This gives,
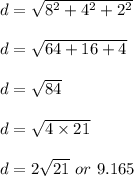
Therefore, the diagonal of the given regular solid is