Question

Need help with linear systems

Answer 1

The minimum value of C is 20

Explanation:

we have

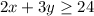`2x+3y\geq 24` ----> constraint 1

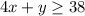`4x+y\geq 38` ----> constraint 2

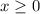`x\geq 0` ----> constraint 3

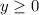`y\geq 0` ----> constraint 4

using a graphing tool

The solution is the shaded area

see the attached figure

To find the minimum value of C evaluate the vertices (9,2) and (12,0) of the solution area in the objective function
`C=2x+y`

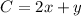
so

For x=9, y=2 --->
`C=2(9)+2=20`

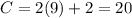
For x=12, y=0 --->
`C=2(12)+0=24`

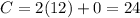
therefore

The minimum value of C is 20