Question

Solve the problem as directed.

The volume (v) of a sphere varies directly as the cube of its diameter (d). Write this statement in algebraic language,
using an equation with the variables c, v, and d.

Answer 1

The algebraic equation for the given statement is
`v = cd^3`

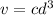
Solution:

Given that The volume (v) of a sphere varies directly as the cube of its diameter (d)

To find: statement in algebraic language using an equation with the variables c, v, and d

Let "v" be the volume of sphere

Let "d" be the diameter of sphere

From given information,

volume of sphere varies directly as the cube of its diameter

`\text{ volume of sphere } \alpha \text{ cube of its diameter}`

`\text{ v} \alpha d^3`

`v = cd^3`

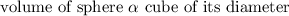
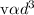
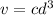
Where "c" is the constant of proportionality

Then the algebraic equation for the given statement will be :-

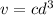`v=cd^3` , where c is the proportionality constant.