Question

An accelerated life test on a large number of type-D alkaline batteries revealed that the mean life for a particular use before they failed is 19.0 hours. The distribution of the lives approximated a normal distribution. The standard deviation of the distribution was 1.2 hours.

About 68.26% of the batteries failed between what two values?

About 95.44% of the batteries failed between what two values?

About 99.97% of the batteries failed between what two values?

Answer 1

About 68.26% of the batteries failed between what two values?

`\mu -\sigma= 19-1.2=17.8, \mu+\sigma=19+1.2=20.2`

About 95.44% of the batteries failed between what two values?

`\mu -2\sigma= 19-2(1.2)=16.6, \mu+2\sigma=19+2(1.2)=21.4`

About 99.97% of the batteries failed between what two values?

14.7 and 23.3

Explanation:

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean".

The empirical rule, also referred to as the three-sigma rule or 68-95-99.7 rule, is a statistical rule which states "that for a normal distribution, almost all data falls within three standard deviations (denoted by σ) of the mean (denoted by µ). Broken down, the empirical rule shows that 68% falls within the first standard deviation (µ ± σ), 95% within the first two standard deviations (µ ± 2σ), and 99.7% within the first three standard deviations (µ ± 3σ)".

Let X the random variable who represent the mean life for a particular use before they failed.

From the problem we have the mean and the standard deviation for the random variable X.
`E(X)=\mu =19.0, Sd(X)=\sigma=1.2`

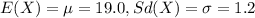
Other way to interpret the empirical rule is like this:

• The probability of obtain values within one deviation from the mean is 0.68

• The probability of obtain values within two deviation's from the mean is 0.95

• The probability of obtain values within three deviation's from the mean is 0.997

About 68.26% of the batteries failed between what two values?

`\mu -\sigma= 19-1.2=17.8, \mu+\sigma=19+1.2=20.2`

We can use the following codes in order to find the limits:

"=NORM.INV(0.1587,19,1.2)" and "=NORM.INV(1-0.1587,19,1.2)"

About 95.44% of the batteries failed between what two values?

`\mu -2\sigma= 19-2(1.2)=16.6, \mu+2\sigma=19+2(1.2)=21.4`

We can use the following codes in order to find the limits:

"=NORM.INV(0.0228;19;1.2)" and "=NORM.INV(1-0.0228;19;1.2)"

About 99.97% of the batteries failed between what two values?

For this case the empirical rule is not the best approximation since within 3 deviations from the mean we have 99.7% of the data and not 99.97%. We can use excel to find the limits.

We can use the following codes in order to find the limits:

"=NORM.INV(0.00015;19;1.2)" and "=NORM.INV(1-0.00015;19;1.2)"

Answer 2

68.2% of the batteries failed between 17.8 and 20.2 hours.

95.44% of the batteries failed between 16.6 and 21.4 hours.

99.97% of the batteries failed between 15.4 and 22.6 hours.

Explanation:

The 68-95-99.7 states that, for a normally distributed sample:

68.26% of the measures are within 1 standard deviation of the sample.

95.44% of the measures are within 2 standard deviations of the sample.

99.97% of the measures are within 3 standard deviations of the sample.

In this problem, we have that:

Mean of 19 hours, standard deviation of 1.2 hours.

About 68.26% of the batteries failed between what two values?

This is within 1 standard deviation of the mean. So 68.2% of the batteries failed between 17.8 and 20.2 hours.

About 95.44% of the batteries failed between what two values?

This is within 2 standard deviations of the mean. So 95.44% of the batteries failed between 16.6 and 21.4 hours.

About 99.97% of the batteries failed between what two values?

This is within 3 standard deviations of the mean. So 99.97% of the batteries failed between 15.4 and 22.6 hours.