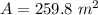Question

Find the area of a regular hexagon with side length 10 m. Round to the nearest tenth.​

Answer 1

`A=259.8\ m^2`

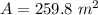
Explanation:

we know that

The area of a regular hexagon is the same that the area of 6 equilateral triangles

The area of 6 equilateral triangles applying the law of sines is equal to

`A=6[(1)/(2)b^2sin(60^o)]`

where

b is the length side of the regular hexagon

we have

`b=10\ m`

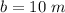
substitute

`A=6[(1)/(2)(10)^2sin(60^o)]`

`A=259.8\ m^2`