Question

A holiday ornament in the shape of a hollow sphere with mass 1.5×10−2 kg and radius 4.5×10−2 m is hung from a tree limb by a small loop of wire attached to the surface of the sphere. If the ornament is displaced a small distance and released, it swings back and forth as a physical pendulum. Calculate its period.

Answer 1

0.55 s

Step-by-step explanation:

We are given that

Mass of holiday ornament=
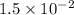`1.5* 10^(-2)`kg

Radius of hollow sphere=
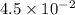`4.5* 10^(-2)` m

We have to find the period of ornament.

Moment of inertia of the sphere about the pivot at the tree limb

`I=(5mR^2)/(3)`

Time period,T=
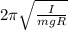
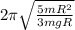
`2\pi\sqrt{(I)/(mgR)}`

T=
`2\pi\sqrt{(5mR^2)/(3mgR)}`

`T=2\pi\sqrt{(5R)/(3g)}`

g=
`9.8m/s^2`

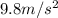
Substitute the values then, we get

`T=2* (22)/(7)* \sqrt{(5* 4.5* 10^(-2))/(3* 9.8)}`

`T=0.55 s`

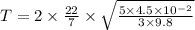
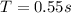
Hence, the time period of ornament=0.55 s