Answer:
80.6 N/m
Step-by-step explanation:
mass (m) = 63 kg
time (s) = 44 s
number of oscillations (n) = 8
stretched length of the cord (L) = 23 m
we can calculate the spring constant of the cord from the formula below
f =
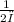 x
x
 ...equation 1
...equation 1
where
f = frequency
k = spring constant
m = mass
frequency =
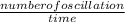
frequency =
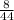 = 0.18
= 0.18
now we can input all the required values into the equation 1
0.18 =
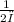 x
x
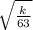
0.18 x 2π =
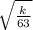
1.13 =
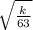
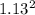 =
=
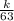
k = 63 x 1.28 = 80.6 N/m