Question

Late one night on a highway, a car speeds by you and fadesinto the distance. Under these conditions the pupils of your eyes(average refractive index = 1.36) have diameters of about6.0 mm. The taillights of this car areseparated by a distance of 1.4 m andemit red light (wavelength = 660 nm in vacuum). How far away fromyou is this car when its taillights appear to merge into a singlespot of light because of the effects of diffraction?

Answer 1

10432.19076 m

Step-by-step explanation:

`\lambda` = Wavelength = 660 nm

d = Diameter of pupils = 6 mm

s = Distance between lights = 1.4 m

L = Distance from observer

From Rayleigh's criteria we have

`1.22\lambda=dsin\theta`

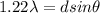
As
`\theta` is small
`sin\theta=(s)/(L)`

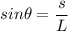
So, the equation becomes

`1.22\lambda=d(s)/(L)\\\Rightarrow L=(ds)/(1.22\lambda)\\\Rightarrow L=(6* 10^(-3)* 1.4)/(1.22* 660* 10^(-9))\\\Rightarrow L=10432.19076\ m`

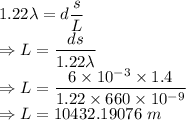
The car is 10432.19076 m from me