Ratio of the area of the square to the area of the circle is

In terms of fraction
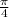
Solution:
Given that perimeter of a particular square and the circumference of a particular circle are equal
To find: ratio of the area of the square to the area of the circle
Let the side of square be "a" and radius of circle be "r"
The perimeter of square is given as:
Perimeter of square = 4a
The circumference of circle is given as:
Circumference of circle = 2πr
From given,
perimeter of a particular square and the circumference of a particular circle are equal
perimeter of a particular square = circumference of a particular circle
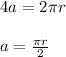
We need to find the ratio of the area of the square to the area of the circle.
We know that,
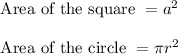
Ratio of area of square to area of circle =
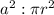
Substituting the value of
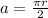 in above ratio,
in above ratio,
Ratio of area of square to area of circle =
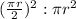
On reducing to lowest terms we get,
⇒
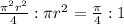
In terms of fraction we get,
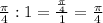
Thus ratio of the area of the square to the area of the circle is
