Answer:
Option A is correct
A. Neither
Explanation:
Given:
Two points are given (2, 15) and (0, 5)
Let
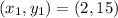 and
and
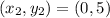
The slope of the line
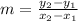
Put all known value in above equation.
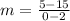
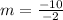
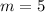
So the slope of the line
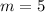 .
.
The equation of the is
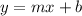 -------------------(1)
-------------------(1)
Where m is the slope of the line and b is y-intercept of the line.
Take point (0, 5) to compute the value of b.
Put
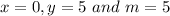 in equation 1.
in equation 1.
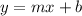
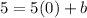
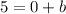
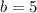
Take point (2, 15) to compute the value of b.
Put
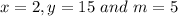 in equation 1.
in equation 1.
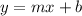
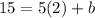
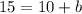
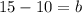
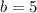
So the equation of the line is.
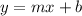
Put m and b value in above equation.
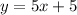 ------------(2)
------------(2)
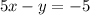
add 10 both side in equation 2.
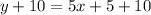
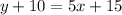
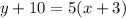
So the equation of line that passes through the point (2,15) and (0,5) is.
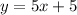 or
or
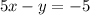 or
or
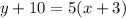
Therefore, Neither the following equations represents a line that passes through the points (2,15) and (0,5).