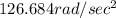Question

Modern wind turbines are larger than they appear, and despite their apparently lazy motion, the speed of the blades tips can be quite high-many times higher than the wind speed. A turbine has blades 59 m long that spin at 14 rpm.

At the tip of a blade, what is the centripetal acceleration?

Answer 1

Centripetal acceleration will be equal to
`126.684rad/sec^2`

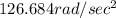
Step-by-step explanation:

We have given length of the blade , that is radius r = 59 m

Angular speed
`\omega =14rpm=(2* 3.14* 14)/(60)=1.4653rad/sec`

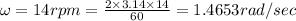
We have to find the centripetal acceleration

We know that centripetal acceleration is given by

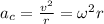`a_c=(v^2)/(r)=\omega ^2r` ( as
`v=\omega r` )

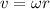So angular acceleration
`a_c=1.4653^2* 59=126.684rad/sec^2`

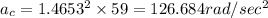
Centripetal; acceleration will be equal to
`126.684rad/sec^2`